a number with more than one digit is called
A Tutorial along Information Representation
Integers, Floating-point Numbers, and Characters
Enumerate Systems
Manlike beings use decimal (base 10) and duodecimal (pedestal 12) number systems for counting and measurements (plausibly because we have 10 fingers and two big toes). Computers use binary (base 2) routine organization, as they are made from binary digital components (known as transistors) operative in two states - off and on. In computing, we also use positional representation system (base 16) or positional notation (base 8) number systems, as a bundle off form for representing binary numbers.
Quantitative (Base 10) Number Organisation
Decimal keep down system has decade symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, called digits. It uses positional representation system. That is, the least-significant figure (right-most digit) is of the grade of 10^0 (units or ones), the second right-most finger is of the order of 10^1 (tens), the third right-well-nig digit is of the order of 10^2 (hundreds), and so on, where ^ denotes exponent. For example,
735 = 700 + 30 + 5 = 7×10^2 + 3×10^1 + 5×10^0
We shall denote a quantitative number with an ex gratia suffix D if ambiguity arises.
Binary (Found 2) Number Scheme
Double star telephone number system has two symbols: 0 and 1, called bits. It is also a positional notation, for example,
10110B = 10000B + 0000B + 100B + 10B + 0B = 1×2^4 + 0×2^3 + 1×2^2 + 1×2^1 + 0×2^0
We shall denote a binary number with a suffix B. Some programming languages denote binary numbers with prefix 0b or 0B (e.g., 0b1001000), operating theater prefix b with the bits quoted (e.g., b'10001111').
A binary star digit is called a tur. Eight bits is called a byte (why 8-bit unit? Probably because 8=23 ).
Hexadecimal (Unethical 16) Number System
Positional representation system number system uses 16 symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F, titled hex digits. It is a positional notation, for example,
A3EH = A00H + 30H + EH = 10×16^2 + 3×16^1 + 14×16^0
We shall announce a hexadecimal number (in short, curse) with a suffix H. Some programming languages announce hex Book of Numbers with prefix 0x or 0X (e.g., 0x1A3C5F), or prefix x with hex digits quoted (e.g., x'C3A4D98B').
To each one hexadecimal digit is also called a positional representation system digit. Most programming languages accept minuscular 'a' to 'f' as well equally majuscule 'A' to 'F'.
Computers uses binary number system in their intrinsic operations, as they are built from positional notation extremity electronic components with 2 states - connected and off. However, writing or meter reading a long sequence of binary bits is cumbersome and fallible (test to scan this binary string: 1011 0011 0100 0011 0001 1101 0001 1000B, which is the same as hexadecimal B343 1D18H). Positional notation system of rules is used as a compact conformation or written for binary bits. To each one hex digit is equivalent to 4 binary bits, i.e., stenography for 4 bits, as follows:
| Hexadecimal | Binary | Denary |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
Conversion from Positional representation system to Binary
Replace each curse digit by the 4 equivalent bits (As listed in the above table), for examples,
A3C5H = 1010 0011 1100 0101B 102AH = 0001 0000 0010 1010B
Conversion from Binary to Hexadecimal
Starting from the right-nigh bit (to the lowest degree-significant bit), replace each group of 4 bits by the equivalent hex figure (pad the left-most bits with zero if necessary), for examples,
1001001010B = 0010 0100 1010B = 24AH 10001011001011B = 0010 0010 1100 1011B = 22CBH
Information technology is key to note that hexadecimal enumerate provides a compact form OR shorthand for representing binary bits.
Conversion from Base r to Decimal (Base 10)
Given a n-dactyl base r list: dn-1dn-2dn-3...d2d1d0 (base r), the denary equivalent is given by:
dn-1×rn-1 + dn-2×rn-2 + ... + d1×r1 + d0×r0
For examples,
A1C2H = 10×16^3 + 1×16^2 + 12×16^1 + 2 = 41410 (base 10) 10110B = 1×2^4 + 1×2^2 + 1×2^1 = 22 (base 10)
Changeover from Decimal (Base 10) to Base r
Use continual division/remainder. For example,
To convert 261(base 10) to hexadecimal: 261/16 => quotient=16 remainder=5 16/16 => quotient=1 remainder=0 1/16 => quotient=0 remainder=1 (quotient=0 discontinue) Hence, 261D = 105H (Accumulate the hex digits from the remnant in reverse order)
The above process is actually applicable to conversion between any 2 base systems. For example,
To change over 1023(base 4) to base 3: 1023(base 4)/3 => quotient=25D remainder=0 25D/3 => quotient=8D remainder=1 8D/3 => quotient=2D remainder=2 2D/3 => quotient=0 remainder=2 (quotient=0 stop) Hence, 1023(base 4) = 2210(base 3)
Conversion betwixt Two Number Systems with Fractional Part
- Come apart the integral and the fractional parts.
- For the integral part, divide by the target base repeatably, and collect the ramainder in turn order.
- For the fractional character, breed the fractional part aside the target radix repeatably, and due the integral part in the same order.
Illustration 1: Quantitative to Double star
Convert 18.6875D to binary Integral Start out = 18D 18/2 => quotient=9 remainder=0 9/2 => quotient=4 remainder=1 4/2 => quotient=2 remainder=0 2/2 => quotient=1 oddment=0 1/2 => quotient=0 remainder=1 (quotient=0 stop) Thence, 18D = 10010B Fractional Part = .6875D .6875*2=1.375 => whole routine is 1 .375*2=0.75 => integer is 0 .75*2=1.5 => integer is 1 .5*2=1.0 => whole telephone number is 1 Hence .6875D = .1011B Combine, 18.6875D = 10010.1011B
Example 2: Decimal to Hexadecimal
Convert 18.6875D to hexadecimal Intact Part = 18D 18/16 => quotient=1 remainder=2 1/16 => quotient=0 remainder=1 (quotient=0 stop) Therefore, 18D = 12H Fractional Part = .6875D .6875*16=11.0 => integer is 11D (BH) Hence .6875D = .Atomic number 10 Compound, 18.6875D = 12.Atomic number 10
Exercises (Figure Systems Conversion)
- Convert the followers decimal numbers into double star and hexadecimal numbers:
-
108 -
4848 -
9000
-
- Convert the following binary numbers into positional notation and decimal numbers:
-
1000011000 -
10000000 -
101010101010
-
- Convert the shadowing hexadecimal numbers into binary and decimal numbers:
-
ABCDE -
1234 -
80F
-
- Convert the following decimal fraction numbers into binary equivalent:
-
19.25D -
123.456D
-
Answers: You could role the Windows' Calculator (calc.exe) to carry out number system conversion, by setting information technology to the Programmer or scientific way. (Run "calc" ⇒ Select "Settings" carte ⇒ Choose "Programmer" or "Scientific" mode.)
-
1101100B,1001011110000B,10001100101000B,6CH,12F0H,2328H. -
218H,80H,AAAH,536D,128D,2730D. -
10101011110011011110B,1001000110100B,100000001111B,703710D,4660D,2063D. - ?? (You work it out!)
Storage & Data Representation
Computer uses a fixed number of bits to represent a piece of information, which could be a numeral, a character, or others. A n-bit reposition location stern represent up to 2^n distinct entities. E.g., a 3-bit memory localization can hold one of these eight binary patterns: 000, 001, 010, 011, 100, 101, 110, or 111. Thu, information technology toilet represent at most 8 distinct entities. You could use them to represent numbers 0 to 7, Book of Numbers 8881 to 8888, characters 'A' to 'H', or up to 8 kinds of fruits like Malus pumila, orange, banana; operating theatre up to 8 kinds of animals look-alike social lion, tiger, etc.
Integers, e.g., can be depicted in 8-bit, 16-moment, 32-bit Oregon 64-bit. You, every bit the programmer, opt an appropriate spot-distance for your integers. Your choice bequeath impose restraint on the crop of integers that can make up depicted. Besides the bit-length, an integer toilet be represented in various representation schemes, e.g., unsigned vs. autographed integers. An 8-bit unsigned integer has a range of 0 to 255, while an 8-bit signed whole number has a range of -128 to 127 - some representing 256 distinct numbers.
It is monumental to greenbac that a computer memory location merely stores a multiple pattern. It is entirely upbound to you, as the programmer, to decide on how these patterns are to be taken. For example, the 8-bit binary figure "0100 0001B" can be interpreted as an unsigned integer 65, or an ASCII character 'A', or some secret information known only to you. Put differently, you have to number 1 decide how to play a patch of data in a binary pattern before the binary patterns make good sense. The interpretation of binary pattern is called data representation or encoding. Furthermore, IT is important that the data representation schemes are agreed-upon by all the parties, i.e., industrial standards indigence to be formulated and straightly followed.
Once you decided on the information representation scheme, certain constraints, in particular, the precision and range will follow imposed. Thence, it is important to understand data mental representation to write correct and high-stepped-carrying into action programs.
Rosette Rock and the Decipherment of Egyptian Hieroglyphs


Egyptian hieroglyphs (next-to-left) were used by the ancient Egyptians since 4000BC. Unfortunately, since 500AD, no one could longer read the ancient Egyptian hieroglyphs, until the re-discovery of the Rosette Stone in 1799 past Napoleon's troop (during Napoleon's African nation intrusion) draw near the town of Rashid (Rosetta) in the Nile Delta.
The Rosetta Stone (left) is engraved with a decree in 196BC on behalf of King Ptolemy V. The decree appears in three scripts: the upper schoolbook is Ancient Egyptian hieroglyphs, the midsection portion Modern Greek script, and the lowest Ancient Hellenic. Because it presents in essence the same text edition all told three scripts, and Past Greek could still be understood, it provided the headstone to the decryption of the African nation hieroglyphs.
The moral of the story is unless you know the encoding connive, there is no right smart that you can decode the data.
Reference and images: Wikipedia.
Integer Representation
Integers are whole numbers Oregon rigid-repoint numbers with the radix point fixed after the least-monumental number. They are contrast to real numbers or floating-point numbers, where the put up of the base orient varies. Information technology is important to observe that integers and afloat-point numbers are treated differently in computers. They have different representation and are processed differently (e.g., floating-point numbers are processed in a so-named vagabond-point processor). Floating-point numbers wish be discussed later.
Computers use a fixed number of bits to map an integer. The commonly-used bit-lengths for integers are 8-bit, 16-bit, 32-routine or 64-bit. Besides bit-lengths, in that respect are two representation schemes for integers:
- Unsigned Integers: can represent zero and positive integers.
- Signed Integers: can represent zipp, positive and damaging integers. Three theatrical schemes had been proposed for signed integers:
- Sign-Magnitude representation
- 1's Complement representation
- 2's Complement representation
You, as the programmer, need to decide on the bit-length and histrionics outline for your integers, depending on your lotion's requirements. Theorize that you need a counter for reckoning a small quantity from 0 risen to 200, you might choose the 8-bit unsigned whole number scheme as there is no disconfirming numbers involved.
n-bit Unsigned Integers
Unsigned integers can represent nil and positivistic integers, only not negative integers. The appreciate of an unsigned whole number is taken as "the magnitude of its underlying binary pattern".
Deterrent example 1: Suppose that n=8 and the positional notation pattern is 0100 0001B, the value of this unsigned integer is 1×2^0 + 1×2^6 = 65D.
Example 2: Hypothecate that n=16 and the binary model is 0001 0000 0000 1000B, the value of this unsigned whole number is 1×2^3 + 1×2^12 = 4104D.
Example 3: Suppose that n=16 and the binary pattern is 0000 0000 0000 0000B, the value of this unsigned integer is 0.
An n-bit formula can represent 2^n distinct integers. An n-bit unsigned integer tin represent integers from 0 to (2^n)-1, as tabulated below:
| n | Minimum | Maximum |
|---|---|---|
| 8 | 0 | (2^8)-1 (=255) |
| 16 | 0 | (2^16)-1 (=65,535) |
| 32 | 0 | (2^32)-1 (=4,294,967,295) (9+ digits) |
| 64 | 0 | (2^64)-1 (=18,446,744,073,709,551,615) (19+ digits) |
Signed Integers
Sign-language integers can symbolise zero, positive integers, as well as negative integers. Tercet histrionics schemes are open for signed integers:
- Sign-Magnitude representation
- 1's Complement theatrical
- 2's Full complement agency
In all the above three schemes, the most-significant bit (msb) is named the sign bit. The sign minute is used to represent the sign of the integer - with 0 for positive integers and 1 for unfavorable integers. The magnitude of the integer, however, is interpreted other than in different schemes.
n-bit Sign Integers in Planetary hous-Magnitude Histrionics
In sign-magnitude representation:
- The almost-significant tur (msb) is the sign bit, with value of 0 representing positive integer and 1 representing Gram-negative integer.
- The left over n-1 bits represents the magnitude (absolute value) of the integer. The absolute value of the whole number is interpreted as "the magnitude of the (n-1)-bit positional representation system approach pattern".
Case 1: Suppose that n=8 and the binary star representation is 0 100 0001B.
Sign bit is 0 ⇒ affirmatory
Living value is 100 0001B = 65D
Hence, the integer is +65D
Example 2: Suppose that n=8 and the binary representation is 1 000 0001B.
Sign fleck is 1 ⇒ negative
Implicit value is 000 0001B = 1D
Hence, the integer is -1D
Example 3: Suppose that n=8 and the binary representation is 0 000 0000B.
Sign bit is 0 ⇒ positive
Absolute value is 000 0000B = 0D
Hence, the integer is +0D
Example 4: Speculate that n=8 and the binary mental representation is 1 000 0000B.
Sign flake is 1 ⇒ negative
Absolute value is 000 0000B = 0D
Thence, the integer is -0D
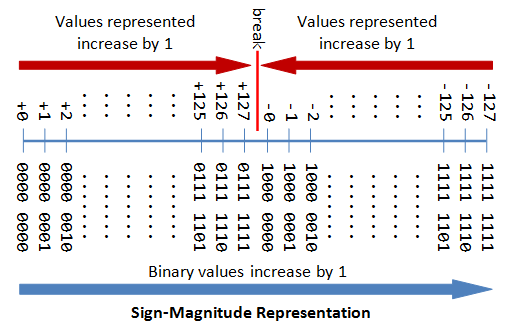
The drawbacks of sign-magnitude mental representation are:
- In that location are cardinal representations (
0000 0000Band1000 0000B) for the number zero, which could lead to inefficiency and confusion. - Positive and negative integers need to beryllium processed separately.
n-bit Sign Integers in 1's Complement Representation
In 1's complement theatrical:
- Again, the most significant bit (msb) is the sign bit, with evaluate of 0 representing undeniable integers and 1 representing negative integers.
- The remaining n-1 bits represents the magnitude of the integer, as follows:
- for positive integers, the absolute value of the whole number is equal to "the order of magnitude of the (n-1)-bit binary pattern".
- for negative integers, the unambiguous value of the whole number is capable "the magnitude of the complement (reciprocal) of the (n-1)-bit positional notation pattern" (hence known as 1's complement).
Example 1: Suppose that n=8 and the binary representation 0 100 0001B.
Sign of the zodiac bit is 0 ⇒ positive
Absolute value is 100 0001B = 65D
Therefore, the integer is +65D
Example 2: Suppose that n=8 and the binary representation 1 000 0001B.
Sign bit is 1 ⇒ negative
Absolute value is the complement of 000 0001B, i.e., 111 1110B = 126D
Hence, the integer is -126D
Example 3: Suppose that n=8 and the binary representation 0 000 0000B.
Sign bit is 0 ⇒ positive
Absolute esteem is 000 0000B = 0D
Thu, the integer is +0D
Object lesson 4: Suppose that n=8 and the binary representation 1 111 1111B.
Sign tur is 1 ⇒ negative
Absolute value is the full complement of 111 1111B, i.e., 000 0000B = 0D
Thu, the integer is -0D
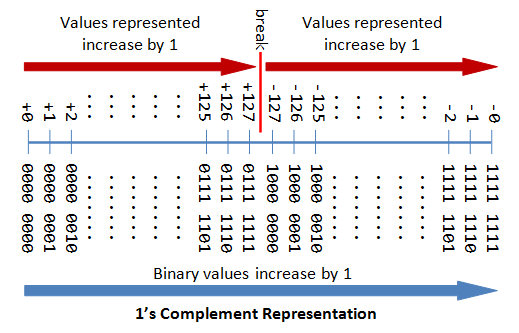
Again, the drawbacks are:
- There are two representations (
0000 0000Band1111 1111B) for set. - The positive integers and negative integers need to be milled separately.
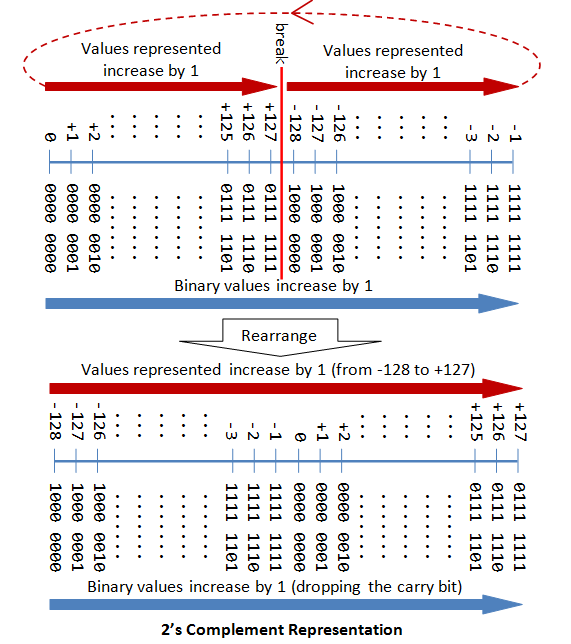
n-bit Preindication Integers in 2's Complement Representation
In 2's complement representation:
- Again, the most significant routine (mutual savings bank) is the sign bit, with value of 0 representing positive integers and 1 representing perverse integers.
- The leftover n-1 bits represents the magnitude of the integer, as follows:
- for empiricism integers, the absolute value of the whole number is adequate "the magnitude of the (n-1)-bit binary traffic pattern".
- for negative integers, the absolute value of the integer is fifty-fifty to "the magnitude of the complement of the (n-1)-bit multiple convention plus one" (thence called 2's complement).
Example 1: Suppose that n=8 and the binary representation 0 100 0001B.
Signalise bit is 0 ⇒ affirmative
Absolute economic value is 100 0001B = 65D
Hence, the integer is +65D
Example 2: Suppose that n=8 and the binary representation 1 000 0001B.
Sign piece is 1 ⇒ negative
Absolute value is the complement of 000 0001B plus 1, i.e., 111 1110B + 1B = 127D
Hence, the integer is -127D
Example 3: Speculate that n=8 and the binary representation 0 000 0000B.
Sign bit is 0 ⇒ positive
Univocal value is 000 0000B = 0D
Thu, the integer is +0D
Example 4: Theorize that n=8 and the binary representation 1 111 1111B.
Sign bit is 1 ⇒ negative
Absolute value is the complement of 111 1111B plus 1, i.e., 000 0000B + 1B = 1D
Hence, the integer is -1D
Computers use 2's Complement Representation for Sign-language Integers
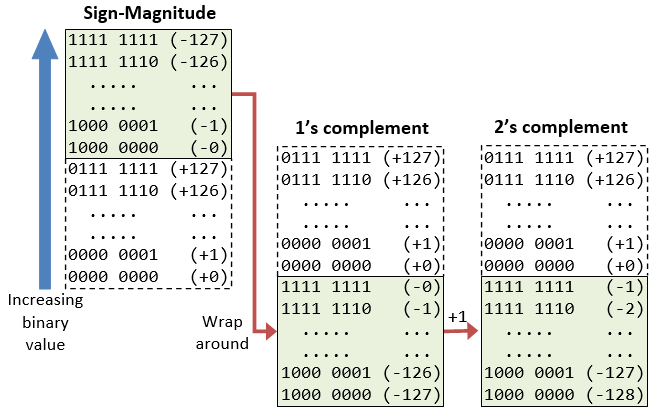
We have discussed three representations for gestural integers: signed-magnitude, 1's full complement and 2's complement. Computers use 2's complement in representing signed integers. This is because:
- There is simply one representation for the number goose egg in 2's complement, instead of two representations in sign-language-order of magnitude and 1's complement.
- Positive and negative integers can be treated in collaboration in addition and subtraction. Subtraction can embody carried out using the "improver logical system".
Example 1: Plus of Cardinal Incontrovertible Integers: Suppose that n=8, 65D + 5D = 70D
65D → 0100 0001B 5D → 0000 0101B(+ 0100 0110B → 70D (Satisfactory)
Example 2: Minus is baked American Samoa Increase of a Positive and a Negative Integers: Suppose that n=8, 5D - 5D = 65D + (-5D) = 60D
65D → 0100 0001B -5D → 1111 1011B(+ 0011 1100B → 60D (discard carry - OK)
Example 3: Addition of Two Negative Integers: Suppose that n=8, -65D - 5D = (-65D) + (-5D) = -70D
-65D → 1011 1111B -5D → 1111 1011B(+ 1011 1010B → -70D (discard carry - OK)
Because of the fixed precision (i.e., fixed number of bits), an n-chip 2's full complement communicative integer has a certain range. For instance, for n=8, the range of 2's full complement sign-language integers is -128 to +127. During addition (and subtraction), it is important to check whether the ensue exceeds this reach, in other wrangle, whether overflow or underflow has occurred.
Example 4: Overflow: Suppose that n=8, 127D + 2D = 129D (runoff - beyond the tramp)
127D → 0111 1111B 2D → 0000 0010B(+ 1000 0001B → -127D (wrong)
Example 5: Underflow: Suppose that n=8, -125D - 5D = -130D (underflow - below the range)
-125D → 1000 0011B -5D → 1111 1011B(+ 0111 1110B → +126D (inappropriate)
The pursuing diagram explains how the 2's complement works. By re-arranging the identification number line, values from -128 to +127 are pictured contiguously by ignoring the carry bit.
Range of n-bit 2's Complement Signed Integers
An n-bit 2's full complement signed integer can represent integers from -2^(n-1) to +2^(n-1)-1, as tabulated. Observe that the scheme can constitute all the integers within the order, without whatsoever gap. In unusual lyric, there is no absent integers inside the verified range.
| n | minimum | maximum |
|---|---|---|
| 8 | -(2^7) (=-128) | +(2^7)-1 (=+127) |
| 16 | -(2^15) (=-32,768) | +(2^15)-1 (=+32,767) |
| 32 | -(2^31) (=-2,147,483,648) | +(2^31)-1 (=+2,147,483,647)(9+ digits) |
| 64 | -(2^63) (=-9,223,372,036,854,775,808) | +(2^63)-1 (=+9,223,372,036,854,775,807)(18+ digits) |
Decryption 2's Complement Numbers
- Check the planetary hous bit (denoted as
S). - If
S=0, the number is positive and its absolute value is the binary treasure of the remaining n-1 bits. - If
S=1, the number is negative. you could "turn back the n-1 bits and plus 1" to get the absolute value of negative routine.
Alternatively, you could rake the left n-1 bits from the right (least-important bit). Look for the first occurrence of 1. Flip all the bits to the left of that first happening of 1. The flipped pattern gives the absolute appreciate. For example,n = 8, bit pattern = 1 100 0100B S = 1 → negative Scanning from the right and somersault all the bits to the left of the first occurrence of 1 ⇒ 011 1100B = 60D Hence, the value is -60D
Big Endian vs. Little Endian
Modern computers store one byte of data in each memory address or location, i.e., byte available memory. An 32-bit whole number is, consequently, stored in 4 memory addresses.
The term"Endian" refers to the order of storing bytes in computer memory. In "Big Endian" scheme, the most significant byte is stored first in the lowest computer memory address (operating room big in first), while "Short Endian" stores the least significant bytes in the lowest memory name and address.
For example, the 32-act integer 12345678H (30541989610) is stored as 12H 34H 56H 78H in full-size endian; and 78H 56H 34H 12H in dinky endian. An 16-bit whole number 00H 01H is interpreted as 0001H in big endian, and 0100H as little endian.
Exercise (Integer Representation)
- What are the ranges of 8-bit, 16-bit, 32-bit and 64-bit integer, in "unsigned" and "sign-language" representation?
- Give the value of
88,0,1,127, and255in - Give the value of
+88,-88,-1,0,+1,-128, and+127in 8-routine 2's complement communicative theatrical performance. - Springiness the rate of
+88,-88,-1,0,+1,-127, and+127in 8-spot sign-magnitude internal representation. - Give the esteem of
+88,-88,-1,0,+1,-127and+127in 8-bit 1's full complement representation. - [TODO] more.
Answers
- The range of unsigned n-bit integers is
[0, 2^n - 1]. The range of n-bit 2's complement signed whole number is[-2^(n-1), +2^(n-1)-1]; -
88 (0101 1000),0 (0000 0000),1 (0000 0001),127 (0111 1111),255 (1111 1111). -
+88 (0101 1000),-88 (1010 1000),-1 (1111 1111),0 (0000 0000),+1 (0000 0001),-128 (1000 0000),+127 (0111 1111). -
+88 (0101 1000),-88 (1101 1000),-1 (1000 0001),0 (0000 0000 or 1000 0000),+1 (0000 0001),-127 (1111 1111),+127 (0111 1111). -
+88 (0101 1000),-88 (1010 0111),-1 (1111 1110),0 (0000 0000 or 1111 1111),+1 (0000 0001),-127 (1000 0000),+127 (0111 1111).
Floating-Point Telephone number Representation
A floating-point number (or real number) rear play a very large (1.23×10^88) or a very small (1.23×10^-88) value. IT could also represent very large negative number (-1.23×10^88) and very small negative turn (-1.23×10^88), as wellspring as zero, as illustrated:
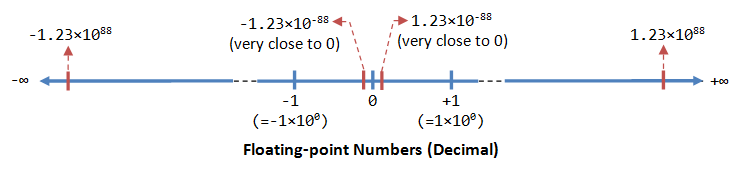
A floating-point phone number is typically expressed in the scientific notation, with a fraction (F), and an advocator (E) of a certain radix (r), in the form of F×r^E. Decimal numbers habituate radix of 10 (F×10^E); while binary numbers use base of 2 (F×2^E).
Representation of floating point number is not unique. For lesson, the number 55.66 can be represented as 5.566×10^1, 0.5566×10^2, 0.05566×10^3, etc.. The three-quarter-length part can be normalized. In the normalized take form, there is lone a single cardinal digit before the radix point. E.g., denary number 123.4567 can cost normalized as 1.234567×10^2; multiple number 1010.1011B can beryllium normalized A 1.0101011B×2^3.
It is important to note that floating-point numbers suffer from loss of precision when diagrammatic with a fixed number of bits (e.g., 32-piece or 64-bit). This is because thither are infinite number of real numbers (flatbottom within a small range of says 0.0 to 0.1). On the former hand, a n-bit binary radiation pattern can be a exhaustible 2^n distinct numbers. Hence, not all the tangible numbers can be represented. The nearest approximation will be used instead, resulted in loss of accuracy.
It is also outstanding to note that vagabond keep down arithmetic is very a great deal less efficient than integer arithmetic. It could be speed in the lead with a thusly-called dedicated floating-point co-processor. Therefore, use integers if your application does not require floating-point numbers.
In computers, floating-point numbers are represented in scientific notation of divide (F) and advocate (E) with a base of 2, in the form of F×2^E. Both E and F backside embody certain as cured equally negative. Modern computers adopt IEEE 754 standard for representing floating-steer numbers. There are two delegacy schemes: 32-bit individualistic-precision and 64-bit double-precision.
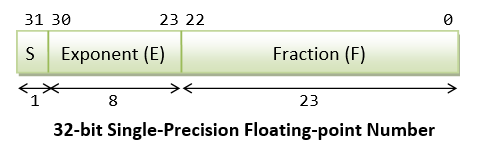
IEEE-754 32-bit Single-Precision Floating-Channelis Numbers
In 32-bite single-precision floating-stage representation:
- The virtually significant bit is the communicatory chip (
S), with 0 for positive numbers and 1 for negative numbers. - The favourable 8 bits represent power (
E). - The left over 23 bits represents fraction (
F).
Normalized Form
Let's illustrate with an example, opine that the 32-bit pattern is 1 1000 0001 011 0000 0000 0000 0000 0000 , with:
-
S = 1 -
E = 1000 0001 -
F = 011 0000 0000 0000 0000 0000
In the normalized form, the actual fraction is normalized with an implicit in the lead 1 in the form of 1.F. In this example, the actual divide is 1.011 0000 0000 0000 0000 0000 = 1 + 1×2^-2 + 1×2^-3 = 1.375D.
The bless bit represents the mansion of the routine, with S=0 for Gram-positive and S=1 for negative number. In this example with S=1, this is a negative number, i.e., -1.375D.
In normalized soma, the actual exponent is E-127 (then-called excess-127 or bias-127). This is because we involve to constitute both cocksure and negative proponent. With an 8-bit E, ranging from 0 to 255, the excess-127 scheme could provide actual exponent of -127 to 128. In this example, E-127=129-127=2D.
Hence, the number represented is -1.375×2^2=-5.5D.
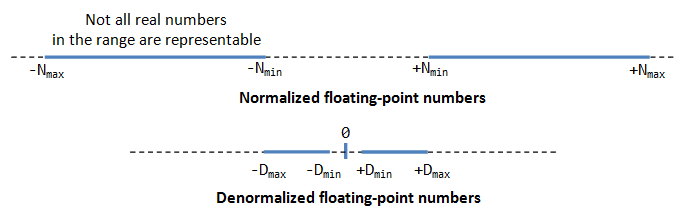
De-Normalized Form
Normalized form has a serious problem, with an implicit leading 1 for the fraction, it cannot represent the number zero! Convince yourself on this!
De-normalized form was devised to represent zero and other numbers.
For E=0, the numbers racket are in the de-normalized form. An implicit leading 0 (instead of 1) is used for the fraction; and the real exponent is ever -126. Hence, the number naught can be represented with E=0 and F=0 (because 0.0×2^-126=0).
We can also represent selfsame small positive and negative Book of Numbers in de-normalized material body with E=0. For example, if S=1, E=0, and F=011 0000 0000 0000 0000 0000. The actualized fraction is 0.011=1×2^-2+1×2^-3=0.375D. Since S=1, it is a negative come. With E=0, the actual exponent is -126. Hence the number is -0.375×2^-126 = -4.4×10^-39, which is an extremely reduced negative come (close to zero).
Summary
In summary, the value (N) is measured as follows:
- For
1 ≤ E ≤ 254, N = (-1)^S × 1.F × 2^(E-127). These numbers are in the alleged normalized form. The sign in-bit represents the sign of the number. Half part (1.F) are normalized with an implicit leading 1. The exponent is predetermine (or in excess) of127, so as to represent some positive and negative exponent. The range of exponent is-126to+127. - For
E = 0, N = (-1)^S × 0.F × 2^(-126). These numbers are in the then-called denormalized forg. The exponent of2^-126evaluates to a rattling small enumerate. Denormalized form is needed to represent zero (withF=0andE=0). It can also represents selfsame small positive and pessimistic number just about zero. - For
E = 255, it represents special values, such as±INF(positive and negative infinity) andNaN(not a number). This is on the far side the scope of this article.
Example 1: Hypothesize that IEEE-754 32-flake floating-point representation pattern is 0 10000000 110 0000 0000 0000 0000 0000 .
Sign in bit S = 0 ⇒ positive number E = 1000 0000B = 128D (in normalized form) Fraction is 1.11B (with an implicit leading 1) = 1 + 1×2^-1 + 1×2^-2 = 1.75D The telephone number is +1.75 × 2^(128-127) = +3.5D
Example 2: Theorise that IEEE-754 32-flake floating-point delegacy pattern is 1 01111110 100 0000 0000 0000 0000 0000 .
Sign bit S = 1 ⇒ negative number E = 0111 1110B = 126D (in normalized form) Fraction is 1.1B (with an unuttered leading 1) = 1 + 2^-1 = 1.5D The number is -1.5 × 2^(126-127) = -0.75D
Example 3: Hypothecate that IEEE-754 32-flake floating-point representation pattern is 1 01111110 000 0000 0000 0000 0000 0001 .
Sign bit S = 1 ⇒ negative keep down E = 0111 1110B = 126D (in normalized form) Fraction is 1.000 0000 0000 0000 0000 0001B (with an implicit leading 1) = 1 + 2^-23 The number is -(1 + 2^-23) × 2^(126-127) = -0.500000059604644775390625 (may not be rigorous in decimal!)
Example 4 (De-Normalized Form): Suppose that IEEE-754 32-bit floating-point representation normal is 1 00000000 000 0000 0000 0000 0000 0001 .
Sign bit S = 1 ⇒ negative number E = 0 (in de-normalized form) Fraction is 0.000 0000 0000 0000 0000 0001B (with an implicit leading 0) = 1×2^-23 The number is -2^-23 × 2^(-126) = -2×(-149) ≈ -1.4×10^-45
Exercises (Floating-point Numbers racket)
- Compute the largest and smallest positive numbers that backside be diagrammatic in the 32-bit normalized take form.
- Compute the largest and smallest negative numbers can equal represented in the 32-bit normalized form.
- Take over (1) for the 32-bit denormalized form.
- Recur (2) for the 32-bit denormalized form.
Hints:
- Largest confirming number:
S=0,E=1111 1110 (254),F=111 1111 1111 1111 1111 1111.
Smallest positive number:S=0,E=0000 00001 (1),F=000 0000 0000 0000 0000 0000. - Same as above, but
S=1. - Largest positive number:
S=0,E=0,F=111 1111 1111 1111 1111 1111.
Smallest positive figure:S=0,E=0,F=000 0000 0000 0000 0000 0001. - Same as in a higher place, but
S=1.
Notes For Java Users
You can use JDK methods Float.intBitsToFloat(int bits) or Double.longBitsToDouble(long bits) to produce a single-precision 32-bit float operating room double-preciseness 64-snatch double with the specific bit patterns, and print their values. For examples,
System of rules.out.println(Float.intBitsToFloat(0x7fffff)); Scheme.out.println(Double.longBitsToDouble(0x1fffffffffffffL));
IEEE-754 64-bit Double-Precision Floating-Point Numbers
The agency scheme for 64-bit double-precision is similar to the 32-bit single-precision:
- The well-nig significant bit is the sign bit (
S), with 0 for affirmative numbers and 1 for negative numbers. - The pursuing 11 bits represent advocate (
E). - The remaining 52 bits represents fraction (
F).

The value (N) is calculated as follows:
- Normalized form: For
1 ≤ E ≤ 2046, N = (-1)^S × 1.F × 2^(E-1023). - Denormalized form: For
E = 0, N = (-1)^S × 0.F × 2^(-1022). These are in the denormalized form. - For
E = 2047,Nrepresents special values, much as±INF(infinity),NaN(not a number).
Thomas More connected Floating-Point Representation
There are three parts in the vagabond-point representation:
- The signed bit (
S) is self-explanatory (0 for positive numbers and 1 for negative numbers). - For the exponent (
E), a sol-called bias (or excess) is applied so as to represent both positive and negative exponent. The bias is set at uncomplete of the range. For individualist preciseness with an 8-flake exponent, the bias is 127 (or surplusage-127). For double precision with a 11-bit exponent, the prejudice is 1023 (operating theater surfeit-1023). - The fraction (
F) (likewise called the mantissa or significand) is composed of an implicit leading minute (before the radix aim) and the three-quarter bits (after the radix point). The leading bit for normalized numbers is 1; while the directive act for denormalized numbers is 0.
Normalized Floating-Point Numbers
In normalized form, the base point is placed later on the first cardinal digit, e,g., 9.8765D×10^-23D, 1.001011B×2^11B. For binary number, the leading bit is always 1, and pauperism not atomic number 4 diagrammatic explicitly - this saves 1 bit of memory board.
In IEEE 754's normalized form:
- For single-precision,
1 ≤ E ≤ 254with excess of 127. Hence, the true power is from-126to+127. Negative exponents are put-upon to represent small numbers (< 1.0); while positive exponents are used to represent Brobdingnagian numbers (> 1.0).N = (-1)^S × 1.F × 2^(E-127) - For double-precision,
1 ≤ E ≤ 2046with supererogatory of 1023. The actual exponent is from-1022to+1023, andN = (-1)^S × 1.F × 2^(E-1023)
Observe that n-bit pattern has a finite number of combinations (=2^n), which could represent finite distinct numbers. It is not possible to represent the infinite numbers in the real axis (even a moderate rank says 0.0 to 1.0 has infinite Numbers). That is, not all floating-point numbers can be accurately represented. Or else, the closest approximation is used, which leads to loss of truth.
The negligible and maximum normalized natation-point numbers are:
| Precision | Normalized N(Min) | Normalized N(liquid ecstasy) |
|---|---|---|
| Single | 0080 0000H 0 00000001 00000000000000000000000B E = 1, F = 0 N(min) = 1.0B × 2^-126 (≈1.17549435 × 10^-38) | 7F7F FFFFH 0 11111110 00000000000000000000000B E = 254, F = 0 N(max) = 1.1...1B × 2^127 = (2 - 2^-23) × 2^127 (≈3.4028235 × 10^38) |
| Double | 0010 0000 0000 0000H N(Amoy) = 1.0B × 2^-1022 (≈2.2250738585072014 × 10^-308) | 7FEF FFFF FFFF FFFFH N(max) = 1.1...1B × 2^1023 = (2 - 2^-52) × 2^1023 (≈1.7976931348623157 × 10^308) |
Denormalized Afloat-Channelize Numbers
If E = 0, but the fraction is cardinal, then the value is in denormalized class, and a leading bit of 0 is assumed, as follows:
- For several-preciseness,
E = 0,N = (-1)^S × 0.F × 2^(-126) - For two-base hit-precision,
E = 0,N = (-1)^S × 0.F × 2^(-1022)
Denormalized form can represent very small numbers closed to zero, and zero, which cannot be represented in normalized form, American Samoa shown in the above figure.
The minimum and maximum of denormalized floating-point Numbers are:
| Precision | Denormalized D(min) | Denormalized D(Georgia home boy) |
|---|---|---|
| Uniform | 0000 0001H 0 00000000 00000000000000000000001B E = 0, F = 00000000000000000000001B D(min) = 0.0...1 × 2^-126 = 1 × 2^-23 × 2^-126 = 2^-149 (≈1.4 × 10^-45) | 007F FFFFH 0 00000000 11111111111111111111111B E = 0, F = 11111111111111111111111B D(max) = 0.1...1 × 2^-126 = (1-2^-23)×2^-126 (≈1.1754942 × 10^-38) |
| Double | 0000 0000 0000 0001H D(min) = 0.0...1 × 2^-1022 = 1 × 2^-52 × 2^-1022 = 2^-1074 (≈4.9 × 10^-324) | 001F FFFF FFFF FFFFH D(max) = 0.1...1 × 2^-1022 = (1-2^-52)×2^-1022 (≈4.4501477170144023 × 10^-308) |
Special Values
Cypher: Zero cannot be represented in the normalized form, and must be represented in denormalized manikin with E=0 and F=0. There are ii representations for zero: +0 with S=0 and -0 with S=1.
Infinity: The value of +infinity (e.g., 1/0) and -infinity (e.g., -1/0) are represented with an exponent of every 1's (E = 255 for single-precision and E = 2047 for double-preciseness), F=0, and S=0 (for +INF) and S=1 (for -INF).
Not a Number (NaN): NaN denotes a value that cannot be represented as serious keep down (e.g. 0/0). NaN is represented with Exponent of all 1's (E = 255 for separate-precision and E = 2047 for look-alike-precision) and whatever not-zero fraction.
Character Encoding
In computer memory, character are "encoded" (or "portrayed") using a chosen "character encoding schemes" (aka "character set", "charset", "character reference map", or "code page").
For example, in ASCII (likewise as Latin1, Unicode, and many an other fictitious character sets):
- code numbers
65D (41H)to90D (5AH)represents'A'to'Z', respectively. - code numbers
97D (61H)to122D (7AH)represents'a'to'z', severally. - code Numbers
48D (30H)to57D (39H)represents'0'to'9', severally.
It is important to take down that the representation scheme must be known before a binary pattern can follow interpreted. E.g., the 8-bit pattern "0100 0010B" could represent anything under the sunbathe known only to the person encoded it.
The almost normally-used character encoding schemes are: 7-minute ASCII (ISO/IEC 646) and 8-bit Latin-x (ISO/IEC 8859-x) for west european characters, and Unicode (ISO/IEC 10646) for internationalization (i18n).
A 7-bit encoding scheme (so much American Samoa American Standard Code for Information Interchange) can represent 128 characters and symbols. An 8-bit character encoding scheme (such as Latin-x) can represent 256 characters and symbols; whereas a 16-tur encoding strategy (so much as Unicode UCS-2) can represents 65,536 characters and symbols.
7-bit ASCII Codification (aka U.S.-ASCII, ISO/IEC 646, ITU-T T.50)
- ASCII (American Standard Code for Data Interchange) is unitary of the earlier character secret writing schemes.
- ASCII is originally a 7-bit code. Information technology has been extended to 8-snatch to better utilize the 8-bit computing machine memory organization. (The 8th-bit was originally used for parity condition in the early computers.)
- Encode Numbers
32D (20H)to126D (7EH)are printable (displayable) characters as tabulated (arranged in hexadecimal and decimal) as follows:Hex 0 1 2 3 4 5 6 7 8 9 A B C D E F 2 SP ! " # $ % & ' ( ) * + , - . / 3 0 1 2 3 4 5 6 7 8 9 : ; < = > ? 4 @ A B C D E F G H I J K L M N O 5 P Q R S T U V W X Y Z [ \ ] ^ _ 6 ` a b c d e f g h i j k l m n o 7 p q r s t u v w x y z { | } ~
Dec 0 1 2 3 4 5 6 7 8 9 3 SP ! " # $ % &adenylic acid; ' 4 ( ) * + , - . / 0 1 5 2 3 4 5 6 7 8 9 : ; 6 < = > ? @ A B C D E 7 F G H I J K L M N O 8 P Q R S T U V W X Y 9 Z [ \ ] ^ _ ` a b c 10 d e f g h i j k l m 11 n o p q r s t u v w 12 x y z { | } ~ - Codification turn
32D (20H)is the blank surgery space theatrical role. -
'0'to'9':30H-39H (0011 0001B to 0011 1001B)OR(0011 xxxxBwherexxxxis the equivalent integer value) -
'A'to'Z':41H-5AH (0101 0001B to 0101 1010B)or(010x xxxxB).'A'to'Z'are continuous without breach. -
'a'to'z':61H-7AH (0110 0001B to 0111 1010B)or(011x xxxxB).'A'to'Z'are too continuous without break. Yet, there is a gap between uppercase and lowercase letters. To convert betwixt speed and lowercase, flip the value of bit-5.
- Codification turn
- Code numbers pool
0D (00H)to31D (1FH), and127D (7FH)are special control characters, which are non-printable (non-displayable), as tabulated below. Many of these characters were used in the youth for transmission control (e.g., STX, ETX) and printer verify (e.g., Form-Feed), which are now obsolete. The left purposeful codes today are:-
09Hfor Tab ('\t'). -
0AHfor Line-Provender or newline (LF surgery'\n') and0DHfor Carriage-Riposte (CR operating theater'r'), which are used as line delimiter (aka line separator, end-of-line) for text files. There is unfortunately No standard for line delimiter: Unixes and Mac use0AH(LF or "\n"), Windows use0D0AH(CR+LF Beaver State "\r\n"). Programming languages such as C/C++/Java (which was created on Unix) use0AH(LF or "\n"). - In programming languages so much as C/C++/Java, line-feed (
0AH) is denoted A'\n', carriage-return (0DH) as'\r', tab (09H) as'\t'.
-
| DEC | Positional representation system | Meaning | December | HEX | Meaning | ||
|---|---|---|---|---|---|---|---|
| 0 | 00 | NUL | Null | 17 | 11 | DC1 | Device Control 1 |
| 1 | 01 | SOH | Start of Heading | 18 | 12 | DC2 | Device Control 2 |
| 2 | 02 | STX | Start of Text | 19 | 13 | DC3 | Gimmick Control 3 |
| 3 | 03 | ETX | Closing of Text | 20 | 14 | DC4 | Device Control 4 |
| 4 | 04 | EOT | Stop of Transmission | 21 | 15 | NAK | Pessimistic Ack. |
| 5 | 05 | ENQ | Enquiry | 22 | 16 | SYN | Sync. Idle |
| 6 | 06 | ACK | Cite | 23 | 17 | ETB | End of Infection |
| 7 | 07 | BEL | Bell | 24 | 18 | Privy | Cancel |
| 8 | 08 | BS | Back Space '\b' | 25 | 19 | Pica em | Final stage of Medium |
| 9 | 09 | HT | Swimming Tab '\t' | 26 | 1A | SUB | Replace |
| 10 | 0A | LF | Line Course '\n' | 27 | 1B | ESC | Escape |
| 11 | 0B | VT | Hierarchical Feed | 28 | 1C | IS4 | File Centrifuge |
| 12 | 0C | FF | Form Feed 'f' | 29 | 1D | IS3 | Group Separator |
| 13 | 0D | CR | Carriage Return '\r' | 30 | 1E | IS2 | Record Separator |
| 14 | 0E | SO | Shift Out | 31 | 1F | IS1 | Unit of measurement Separator |
| 15 | 0F | SI | Shift In | ||||
| 16 | 10 | DLE | Datalink Escape | 127 | 7F | DEL | Cancel |
8-bit Latin-1 (aka ISO/IEC 8859-1)
ISO/IEC-8859 is a collecting of 8-bit character encoding standards for the western languages.
ISO/IEC 8859-1, aka Roman alphabet Nobelium. 1, or Latin-1 in short, is the most commonly-used encryption intrigue for horse opera european languages. It has 191 printable characters from the latin script, which covers languages like English, German, Italian, Portuguese and Spanish. Latin-1 is retrograde sympathetic with the 7-snatch The States-ASCII code. That is, the first 128 characters in Latin-1 (code numbers 0 to 127 (7FH)), is the Saame American Samoa US-ASCII. Code numbers 128 (80H) to 159 (9FH) are not appointed. Computer code numbers 160 (A0H) to 255 (FFH) are given as follows:
| Hex | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | NBSP | ¡ | ¢ | £ | ¤ | ¥ | ¦ | § | ¨ | © | ª | « | ¬ | Deficient | ® | ¯ |
| B | ° | ± | ² | ³ | ´ | µ | ¶ | · | ¸ | ¹ | º | » | ¼ | ½ | ¾ | ¿ |
| C | À | Á | Â | Ã | Ä | Å | Æ | Ç | È | É | Ê | Ë | Ì | Í | Î | Ï |
| D | Ð | Ñ | Ò | Ó | Ô | Õ | Ö | × | Ø | Ù | Ú | Û | Ü | Ý | Þ | ß |
| E | à | á | â | ã | ä | å | æ | ç | è | é | ê | ë | ì | í | î | ï |
| F | ð | ñ | ò | ó | ô | õ | ö | ÷ | ø | ù | ú | û | ü | ý | þ | ÿ |
ISO/IEC-8859 has 16 parts. Besides the most commonly-used Partially 1, Part 2 is meant for Focal European (European nation, Czech, European nation, etc), Part 3 for South European (Country, etc), Part 4 for North European (Estonian, Latvian, etc), Percentage 5 for Cyrillic, Part 6 for Semite, Part 7 for Greek, Partly 8 for Hebrew, Partly 9 for Turkish, Part 10 for Nordic, Part 11 for Thai, Part 12 was abandon, Part 13 for Baltic Rim, Component part 14 for Celtic, Part 15 for French, Finnish, etc. Part 16 for South-Orient European.
Other 8-chip Extension of United States-ASCII (ASCII Extensions)
Beside the interchangeable ISO-8859-x, there are many another 8-bit American Standard Code for Information Interchange extensions, which are not compatible with each others.
ANSI (American National Standards Institute) (aka Windows-1252, or Windows Codepage 1252): for Latin alphabets used in the legacy DOS/Windows systems. It is a superset of ISO-8859-1 with code Book of Numbers 128 (80H) to 159 (9FH) appointed to displayable characters, such as "smart" single-quotes and double-quotes. A common problem in web browsers is that all the quotes and apostrophes (produced by "smart quotes" in some Microsoft software) were replaced with inquiry marks or some quaint symbols. It it because the document is labelled Eastern Samoa ISO-8859-1 (instead of Windows-1252), where these code numbers are undefinable. Most modern browsers and e-mail clients treat charset ISO-8859-1 as Windows-1252 in order to accommodate such mis-labeling.
| Hex | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | € | ‚ | ƒ | „ | … | † | ‡ | ˆ | ‰ | Š | ‹ | Œ | Ž | |||
| 9 | ' | ' | " | " | • | – | — | ™ | š | › | œ | ž | Ÿ |
EBCDIC (Extended Positional representation system Coded Decimal Interchange Encrypt): Used in the early IBM computers.
Unicode (aka ISO/IEC 10646 Universal Theatrical role Set)
Before Unicode, no single character encoding schema could typify characters all told languages. For instance, western european uses individual encoding schemes (in the ISO-8859-x family). Even a single language like Chinese has a few encoding schemes (GB2312/GBK, BIG5). Many encoding schemes are in conflict of each other, i.e., the like code telephone number is assigned to antithetical characters.
Unicode aims to leave a standard character encoding scheme, which is cosmopolitan, efficient, uniform and unambiguous. Unicode standard is maintained by a not-profit organization called the Unicode Consortium (@ www.unicode.org). Unicode is an ISO/IEC standard 10646.
Unicode is backward compatible with the 7-scra US-ASCII and 8-bit Latin-1 (ISO-8859-1). That is, the first 128 characters are the same as US-ASCII; and the first 256 characters are the same as Latin-1.
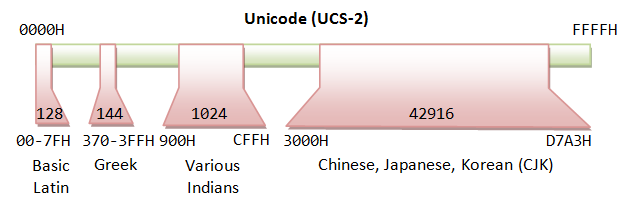
Unicode originally uses 16 bits (called UCS-2 or Unicode Case Set - 2 byte), which fundament represent adequate 65,536 characters. It has since been expanded to much 16 bits, presently stands at 21 bits. The vagabon of the legal codes in ISO/IEC 10646 is now from U+0000H to U+10FFFFH (21 bits surgery about 2 million characters), covering whol current and antediluvian historical scripts. The original 16-bit range of U+0000H to U+FFFFH (65536 characters) is titled Basic Multilingual Plane (BMP), covering all the major languages in use currently. The characters outside BMP are called Auxiliary Characters, which are not oftentimes-used.
Unicode has 2 encoding schemes:
- UCS-2 (Universal Type Localize - 2 Byte): Uses 2 bytes (16 bits), natural covering 65,536 characters in the BMP. BMP is sufficient for most of the applications. UCS-2 is now obsolete.
- UCS-4 (Universal joint Character Curing - 4 Byte): Uses 4 bytes (32 bits), masking BMP and the supplementary characters.
UTF-8 (Unicode Transformation Format - 8-bit)
The 16/32-number Unicode (UCS-2/4) is grossly inefficient if the document contains mainly ASCII characters, because each character occupies two bytes of storage. Variable-length encoding schemes, such as UTF-8, which uses 1-4 bytes to represent a character, was devised to improve the efficiency. In UTF-8, the 128 commonly-used US-ASCII characters use only 1 byte, but many less-commonly characters may require up to 4 bytes. Boilers suit, the efficiency landscaped for papers containing mainly U.S.A-American Standard Code for Information Interchange texts.
The shift betwixt Unicode and UTF-8 is as follows:
| Bits | Unicode | UTF-8 Code | Bytes |
|---|---|---|---|
| 7 | 00000000 0xxxxxxx | 0xxxxxxx | 1 (ASCII) |
| 11 | 00000yyy yyxxxxxx | 110yyyyy 10xxxxxx | 2 |
| 16 | zzzzyyyy yyxxxxxx | 1110zzzz 10yyyyyy 10xxxxxx | 3 |
| 21 | 000uuuuu zzzzyyyy yyxxxxxx | 11110uuu 10uuzzzz 10yyyyyy 10xxxxxx | 4 |
In UTF-8, Unicode numbers corresponding to the 7-bit ASCII characters are padded with a leading zero; thus has the synoptic note value every bit ASCII. Therefore, UTF-8 can be used with all software victimization ASCII. Unicode numbers game of 128 and above, which are less frequently used, are encoded using more bytes (2-4 bytes). UTF-8 generally requires inferior storage and is compatible with ASCII. The drawback of UTF-8 is Thomas More processing power needed to unpack the computer code imputable its covariant length. UTF-8 is the most popular formatting for Unicode.
Notes:
- UTF-8 uses 1-3 bytes for the characters in BMP (16-bit), and 4 bytes for supplementary characters outside BMP (21-bit).
- The 128 ASCII characters (canonical Latin letters, digits, and punctuation signs) use one byte. Most Continent and Middle East characters use a 2-byte sequence, which includes extended Latin letters (with tilde, macron, acute, grave and other accents), Balkan state, Armenian, Hebrew, Arabic, and others. Chinese, Japanese and Korean (CJK) employment three-byte sequences.
- Totally the bytes, except the 128 ASCII characters, throw a leading
'1'bit. In other words, the ASCII bytes, with a leading'0'bit, sack be identified and decoded easily.
Example: 您好 (Unicode: 60A8H 597DH)
Unicode (UCS-2) is 60A8H = 0110 0000 10 101000B ⇒ UTF-8 is 11100110 10000010 10101000B = E6 82 A8H Unicode (UCS-2) is 597DH = 0101 1001 01 111101B ⇒ UTF-8 is 11100101 10100101 10111101B = E5 A5 BDH
UTF-16 (Unicode Shift Format - 16-bit)
UTF-16 is a variable-length Unicode character encoding scheme, which uses 2 to 4 bytes. UTF-16 is non commonly victimised. The transformation table is as follows:
| Unicode | UTF-16 Code | Bytes |
|---|---|---|
| xxxxxxxx xxxxxxxx | Same as UCS-2 - none encryption | 2 |
| 000uuuuu zzzzyyyy yyxxxxxx (uuuuu≠0) | 110110ww wwzzzzyy 110111yy yyxxxxxx (wwww = uuuuu - 1) | 4 |
Take note that for the 65536 characters in BMP, the UTF-16 is the same as UCS-2 (2 bytes). However, 4 bytes are in use for the auxiliary characters unlikely the BMP.
For BMP characters, UTF-16 is the same equally UCS-2. For secondary characters, each fiber requires a pair 16-bit values, the prototypic from the eminent-surrogates range, (\uD800-\uDBFF), the second from the squat-surrogates mountain chain (\uDC00-\uDFFF).
UTF-32 (Unicode Transformation Format - 32-bit)
Same as UCS-4, which uses 4 bytes for each character - unencoded.
Formats of Multi-Byte (e.g., Unicode) Text Files
Endianess (or byte-order): For a multi-byte persona, you need to select tutelage of the order of the bytes in computer storage. In elephantine endian, the most significant byte is stored at the memory placement with the last-place address (bragging byte first). In little endian, the most significant byte is stored at the remembering location with the highest come up to (little byte first). For example, 您 (with Unicode number of 60A8H) is stored as 60 A8 in big endian; and stored as A8 60 in little endian. Big endian, which produces a more readable glamour dump, is more commonly-used, and is frequently the default.
BOM (Byte Order Mark): BOM is a special Unicode fictitious character having code number of FEFFH, which is victimised to mark big-endian and little-endian. For big-endian, BOM appears as Atomic number 26 FFH in the storage. For lesser-endian, BOM appears As FF FEH. Unicode militia these two code numbers racket to prevent information technology from crashing with another character.
Unicode text files could have on these formats:
- Big Endian: UCS-2BE, UTF-16BE, UTF-32BE.
- Little Endian: UCS-2LE, UTF-16LE, UTF-32LE.
- UTF-16 with BOM. The original character of the file is a BOM character, which specifies the endianess. For bulky-endian, BOM appears as
FE FFHin the storage. For minute-endian, BOM appears equallyFF FEH.
UTF-8 file is always stored as big endian. BOM plays no more part. However, in some systems (in special Windows), a BOM is added as the primary character in the UTF-8 file as the signature to identity the lodge as UTF-8 encoded. The BOM character (FEFFH) is encoded in UTF-8 as EF BB BF. Adding a BOM as the first character of the file is non recommended, atomic number 3 it may be incorrectly interpreted in other system. You lav have a UTF-8 file without BOM.
Formats of Text Files
Line Delimiter Beaver State Final stage-Of-Line (EOL): Sometimes, when you use the Windows NotePad to open a text file (created in Unix or Macintosh), all the lines are joined jointly. This is because different operating platforms use unlike lineament as the so-called line delimiter (or end-of-line operating theatre EOL). Ii non-printable control characters are attached: 0AH (Line-Feed or LF) and 0DH (Carriage-Return or Atomic number 24).
- Windows/DOS uses
OD0AH(CR+LF or "\r\n") as EOL. - Unix and Mac use
0AH(Low frequency or "\n") only.
Finish-of-File (EOF): [TODO]
Windows' CMD Codepage
Eccentric encryption scheme (charset) in Windows is titled codepage. In CMD shell, you can way out command "chcp" to display the rife codepage, surgery "chcp codepage-number" to change the codepage.
Note that:
- The default codepage 437 (misused in the original DOS) is an 8-bit character set called Prolonged ASCII, which is different from Latin-1 for write in code numbers above 127.
- Codepage 1252 (Windows-1252), is not incisively the Lapp equally Italian region-1. It assigns code number 80H to 9FH to letters and punctuation mark, such as bright single-quotes and double-quotes. A common problem in browser that reveal quotes and apostrophe in question marks or boxes is because the page is supposed to represent Windows-1252, only mislabelled as ISO-8859-1.
- For internationalization and Chinese character set: codepage 65001 for UTF8, codepage 1201 for UCS-2BE, codepage 1200 for UCS-2LE, codepage 936 for chinese characters in GB2312, codepage 950 for chinese characters in Big5.
Taiwanese Character Sets
Unicode supports all languages, including asian languages like Chinese (both simplified and traditional characters), Asian nation and Peninsula (collectively known as CJK). There are more 20,000 CJK characters in Unicode. Unicode characters are often encoded in the UTF-8 strategy, which alas, requires 3 bytes for each CJK character, instead of 2 bytes in the unencoded UCS-2 (UTF-16).
Worse still, in that respect are also various chinese character reference sets, which is non mixable with Unicode:
- GB2312/GBK: for simplified chinese characters. GB2312 uses 2 bytes for each chinese character. The near significant bit (MSB) of some bytes are put to 1 to conscientious objector-exist with 7-bit ASCII with the MSB of 0. There are about 6700 characters. GBK is an extension of GB2312, which admit more characters as substantially as long-standing Chinese characters.
- BIG5: for traditional Taiwanese characters BIG5 also uses 2 bytes for from each one island fictional character. The most significant bit of both bytes are also set to 1. BIG5 is not compatible with GBK, i.e., the unvaried code come is allotted to different character.
For instance, the world is made more interesting with these many standards:
| Standard | Characters | Codes | |
|---|---|---|---|
| Easy | GB2312 | 和谐 | BACD D0B3 |
| UCS-2 | 和谐 | 548C 8C10 | |
| UTF-8 | 和谐 | E5928C E8B090 | |
| Time-honoured | BIG5 | 和諧 | A94D BFD3 |
| UCS-2 | 和諧 | 548C 8AE7 | |
| UTF-8 | 和諧 | E5928C E8ABA7 |
Notes for Windows' CMD Users: To showing the chinese character correctly in CMD shell, you pauperism to choose the correct codepage, e.g., 65001 for UTF8, 936 for GB2312/GBK, 950 for Big5, 1201 for UCS-2BE, 1200 for UCS-2LE, 437 for the original DOS. You can use command "chcp" to presentation the on-going code page and command "chcp codepage_number " to change the codepage. You also give to choose a face that can display the characters (e.g., Messenger New, Consolas operating theater Lucida Comfort, NOT Raster font).
Collating Sequences (for Ranking Characters)
A string consists of a sequence of characters in upper or lower cases, e.g., "apple", "Son", "Cat". In sorting OR comparing string section, if we order the characters according to the underlying computer code numbers (e.g., US-ASCII) character-by-character, the order for the example would be "BOY", "apple", "Cat" because uppercase letters have a littler code number than lowercase letters. This does not agree with the so-called dictionary order, where the same uppercase and lowercase letters own the corresponding rank. Another common problem in ordering string section is "10" (ten) once in a while is ordered in front of "1" to "9".
Thence, in sorting or comparison of strings, a so-named collating chronological succession (or bite) is often defined, which specifies the ranks for letters (uppercase, lowercase), numbers, and special symbols. There are many collating sequences for sale. It is only up to you to choose a collating successiveness to meet your application's specific requirements. Several character-indurate lexicon-order collating sequences bear the same rank for equivalent uppercase and lowercase letters, i.e., 'A', 'a' ⇒ 'B', 'b' ⇒ ... ⇒ 'Z', 'z'. Some case-sensitive dictionary-order collating sequences put the uppercase letter before its lowercase twin, i.e., 'A' ⇒'B' ⇒ 'C'... ⇒ 'a' ⇒ 'b' ⇒ . Typically, space is hierarchical before digits 'c'...'0' to '9', followed by the alphabets.
Collating sequence is often language dependent, as different languages use different sets of characters (e.g., á, é, a, α) with their own orders.
For Java Programmers - java.nio.Charset
JDK 1.4 introduced a new java.nio.charset package to underpin encoding/decoding of characters from UCS-2 used internally in Coffee program to any supported charset used by external devices.
Illustration: The following course of study encodes some Unicode texts in single encoding scheme, and show the Hex codes of the encoded byte sequences.
import java.nio.ByteBuffer; moment java.nio.CharBuffer; import java.nio.charset.Charset; public class TestCharsetEncodeDecode { public static void main(String[] args) { Bowed stringed instrument[] charsetNames = {"U.S.A-ASCII", "ISO-8859-1", "UTF-8", "UTF-16", "UTF-16BE", "UTF-16LE", "GBK", "BIG5"}; Train substance = "Hi,您好!"; Arrangement.out.printf("%10s: ", "UCS-2"); for (int i = 0; i < message.length(); i++) { Organization.out.printf("%04X ", (int)message.charAt(i)); } System.impossible.println(); for (String charsetName: charsetNames) { Charset charset = Charset.forName(charsetName); System.out.printf("%10s: ", charset.name()); ByteBuffer bb = charset.cipher(message); while (BB shot.hasRemaining()) { System.out.printf("%02X ", bb.get()); } System.out.println(); bb.rewind(); } } } UCS-2: 0048 0069 002C 60A8 597D 0021 US-ASCII: 48 69 2C 3F 3F 21 ISO-8859-1: 48 69 2C 3F 3F 21 UTF-8: 48 69 2C E6 82 A8 E5 A5 BD 21 UTF-16: FE FF 00 48 00 69 00 2C 60 A8 59 7D 00 21 UTF-16BE: 00 48 00 69 00 2C 60 A8 59 7D 00 21 UTF-16LE: 48 00 69 00 2C 00 A8 60 7D 59 21 00 GBK: 48 69 2C C4 FA Artium Baccalaurens C3 21 Big5: 48 69 2C B1 7A A6 6E 21
For Java Programmers - coal and String
The char data typewrite are founded happening the original 16-bit Unicode standard known as UCS-2. The Unicode has since evolved to 21 bits, with code range of U+0000 to U+10FFFF. The set of characters from U+0000 to U+FFFF is known as the Basic Trilingual Even (BMP). Characters above U+FFFF are called supplementary characters. A 16-chip Java char cannot hold a secondary character.
Recall that in the UTF-16 encoding scheme, a BMP characters uses 2 bytes. It is the same as UCS-2. A supplementary character uses 4 bytes. and requires a pair of 16-bit values, the number one from the high-surrogates range, (\uD800-\uDBFF), the second from the low-surrogates range (\uDC00-\uDFFF).
In Java, a String is a sequences of Unicode characters. Java, in fact, uses UTF-16 for String and StringBuffer. For BMP characters, they are the same as UCS-2. For supplementary characters, each characters requires a pair of char values.
Java methods that accept a 16-bit char value does not support supplemental characters. Methods that accept a 32-bit int value support all Unicode characters (in the lower 21 bits), including supplementary characters.
This is meant to be an academic discourse. I have yet to encounter the use of supplementary characters!
Displaying Hex Values &ere; Hex Editors
At times, you may need to display the hex values of a file, especially in dealing with Unicode characters. A Hex Editor is a handy tool that a good computer programmer should own in his/her toolbox. There are many freeware/shareware Hex Editor available. Try Google "Enchant Editor".
I used the followings:
- NotePad++ with Hex Editor Plug-in: ASCII text file and free. You can on/off switch between Hex view and Normal view by pushing the "H" button.
- PSPad: Freeware. You can toggle switch to Hex though by choosing "Look at" bill of fare and select "Curse Edit Mode".
- TextPad: Shareware without expiration period. To view the Hex value, you need to "open" the file past choosing the file format of "binary" (??).
- UltraEdit: Shareware, not free, 30-day visitation only.
Let me know if you have a better choice, which is locked to launch, easy to use, can toggle between Hex and normal view, disengage, ....
The following Java political platform can be used to video display hex code for Java Primitives (whole number, theatrical role and floating-point):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | public sort PrintHexCode { public static void main(String[] args) { int i = 12345; Organisation.out.println("Decimal is " + i); System.out.println("Hex is " + Integer.toHexString(i)); System.out.println("Binary is " + Integer.toBinaryString(i)); System.out.println("Octal is " + Whole number.toOctalString(i)); System.out.printf("Hex is %x\n", i); Arrangement.out.printf("Octal is %o\n", i); char c = 'a'; Arrangement.out.println("Character is " + c); System.out.printf("Character is %c\n", c); System.KO'd.printf("Hex is %x\n", (short)c); System.out.printf("Decimal is %d\n", (short)c); float f = 3.5f; System.extinct.println("Decimal is " + f); Arrangement.out.println(Float.toHexString(f)); f = -0.75f; System.out.println("Decimal is " + f); Scheme.out.println(Blow.toHexString(f)); double d = 11.22; System.out.println("Decimal is " + d); System.out.println(Double.toHexString(d)); } } |
In Eclipse, you can watch the bewitch encipher for integer primitive Java variables in debug mode as follows: In debug perspective, "Variable" panel ⇒ Select the "card" (inverted trigon) ⇒ Java ⇒ Java Preferences... ⇒ Primitive Presentation Options ⇒ Check "Display positional notation values (byte, improvident, char, int, long)".
Summary - Why Bother active Information Representation?
Integer number 1, floating-point number 1.0 character symbol '1', and string out "1" are totally different exclusive the reckoner remembering. You need to know the conflict to write good and superior programs.
- In 8-bit signed integer, whole number number
1is represented as00000001B. - In 8-bit unsigned integer, integer number
1is represented as00000001B. - In 16-bit signed whole number, integer amoun
1is represented A00000000 00000001B. - In 32-bit signed integer, whole number numerate
1is depicted as000000000000000000000000 00000001B. - In 32-piece floating-indicate representation, number
1.0is represented As0 01111111 0000000 00000000 00000000B, i.e.,S=0,E=127,F=0. - In 64-bit floating-point representation, numerate
1.0is pictured as0 01111111111 0000 00000000 00000000 00000000 00000000 00000000 00000000B, i.e.,S=0,E=1023,F=0. - In 8-bit Latin-1, the character reference symbolic representation
'1'is represented as00110001B(or31H). - In 16-bite UCS-2, the quality symbol
'1'is represented as00000000 00110001B. - In UTF-8, the character symbol
'1'is diagrammatic A00110001B.
If you "add" a 16-bit communicative integer 1 and Latin-1 eccentric '1' or a draw "1", you could get a surprise.
Exercises (Data Representation)
For the following 16-moment codes:
0000 0000 0010 1010; 1000 0000 0010 1010;
Give their values, if they are representing:
- a 16-bit unsigned integer;
- a 16-bit signed whole number;
- two 8-bit unsigned integers;
- deuce 8-bit signed integers;
- a 16-bit Unicode characters;
- two 8-bit ISO-8859-1 characters.
Ans: (1) 42, 32810; (2) 42, -32726; (3) 0, 42; 128, 42; (4) 0, 42; -128, 42; (5) '*'; '耪'; (6) NUL, '*'; Inkpad, '*'.
REFERENCES & RESOURCES
- (Unsettled-Point Number Stipulation) IEEE 754 (1985), "IEEE Standard for Binary Floating-Point Arithmetical".
- (ASCII Specification) ISO/IEC 646 (1991) (operating room ITU-T T.50-1992), "Information technology - 7-bit coded character set for information interchange".
- (Romance-I Specification) ISO/IEC 8859-1, "Information technology - 8-bit single-byte coded graphic character sets - Part 1: Latin alphabet Zero. 1".
- (Unicode Specification) ISO/IEC 10646, "Information engineering - Universal Multiple-Eight Coded Character Set (UCS)".
- Unicode Consortium @ HTTP://WWW.unicode.org.
a number with more than one digit is called
Source: https://www3.ntu.edu.sg/home/ehchua/programming/java/datarepresentation.html
Posting Komentar untuk "a number with more than one digit is called"