how to know if it is an inverse function
We lie with that the functions are just like a machine or a loge which takes an input rate and gives us extraordinary output value after processing. There should be only one outturn corresponding to one input. Sometimes it can materialize that we have the output, and we neediness to know the input. In much cases, we need to regress whatever the processing was applied on input. Thus it becomes intrinsical to know the reverse of the cognitive process. If that function is mathematical we need to lie with what is the inverse of the function so that we can go back our input. Let's escort inverses and the work in detail.
Introduction to Backward Functions
The figure given below describes a function and its opposite. This function is represented as f(x) and takes some stimulant values and gives an output. The inverse of this function is denoted by f-1(x). For example, let's tell f(x) = 2x. IT doubles the number which is given as input, its inverse should make them half to get back the input. f-1(x) = ![]() .
.

If functions f(x) and g(x) are inverses of from each one other, then f(x) = y only if g(y) = x.
g(f(x)) = x
Rent's say we have a function f(x) = x2. Now we are asked to find out the inverse of this function. This function is squaring its inputs, we know we demand to take back the square root for calculating the inverse.
f-1(x) = √x2
= ±x
We see that there are cardinal answers possible, which one to prefer? In such cases, the inverse is not possible. So, there are things we need to notice for the functions for which inverses are possible.
- Function moldiness cost Bijective(One-One and Onto) for its inverse to exist.
This function has same values at two polar values of input signal. This function is not paragon for calculating inverse.

- We want to spirit for the points which are not in sphere for the inverse. For example, in the previous shell, dismissive values cannot be allowed.
Inverses with Algebraic Methods
The inverses of functions can also represent calculated using algebraic methods. The idea is, to utility the respect of y in place of f(x) and then wor for y. Army of the Pure's see an example to translate it.
Example: Find the inverse of f(x) = 6x + 10.
Solvent:
We know, f(x) = 6x + 10. Permit's substitute y in situ of f(x).
y = 6x + 10
⇒ y – 10 = 6x
⇒ x =
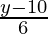
f-1(y) =
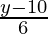
Inverses of Uncouth Functions
The mesa conferred downstairs describes inverses of some common functions which may do in handy while calculating the inverses for complex functions. The table represents the function, its inverse, and its niche cases. Corner cases describe the values which are not allowed as input to the inverse of the function.
| Function | Reverse | Corner Cases |
| Multiplication | Divide | Divide by zero is not allowed |
| Carve up | Multiply | |
| Addition | Subtraction | |
| Subtractions | Addition | |
| xn | | Negative values not allowed when n is even |
| ax | logax | x > 0 and a > 0 |
| goof(x) | sin-1(x) | Only values between -1 to 1 are allowed |
| cos(x) | cos-1(x) | But values between -1 to 1 are allowed |
| tan(x) | tan-1(x) |
Graphs of Opposite Functions
We will get wind the embodiment of the graph of the inverse of a function done an example. Lashkar-e-Toiba's say we have f(x) = ex. Let's say the inverse of this operate is g(x), we know that the inverse of an mathematical notation office is a logarithmic function. So, g(x) = logarithmex. The form below shows the graph for both of the functions.

Notification in the figure, you can see that some the curves are mirror images of all other with respect to the credit line y = x. Then, we can say that the inverse of a function is a mirror see of the function when seen through the line y = x.
Rent's see some problems connected these concepts.
Try out Problems
Interrogate 1: Find the inverse of the office f(x) = ![]()
Solution:
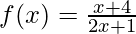
Substituting f(x) with y.
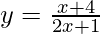
⇒
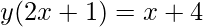
⇒ 2xy + y = x + 4
⇒ x(2y – 1) = 4 – y
⇒ x =
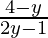
Thus, f-1(y) =
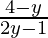
Question 2: Find the inverse of the function f(x) = lnx + 5.
Solvent:
f(x) = lnx + 5
Substituting the f(x) with y
y = lnx + 5
⇒ lnx= y – 5
⇒ x = e(y – 5)
f-1(y) = e(y – 5)
Call into question 3: Find the inverse of the following function and draw its chart.
f(x) = ex + 20
Solution:
f(x) = ex + 20
Substituting the f(x) with y
⇒y = ex + 20
⇒y – 20 = ex
⇒ln(y – 20) = x
f-1(y) = ln(y – 20)
The figure below, shows the graphs for f(x) and it's opposite.

Acknowledge that y > 20 for this function.
Question 4: Land whether the assertion is True or Invalid. For the given function f(x) = x2 + 4, inverse does not exist for complete values of x.
Solution:
We recognize that f(x) = x2 + 4 is not bijective. For example,
f(-2) = 8 and f(2) = 8. So, the opposite for this affair cannot exist for all values of x. Gum olibanum, this command is named Fictitious.
Question 5: Find the inverse for the following subprogram:
f(x) = ![]()
Solution:
f(x) =
Substituting f(x) with y.

⇒

⇒ y(5x + 1) = x
⇒ 5xy + y = x
⇒ x(5y – 1) = -y
⇒ x =
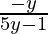
Thusly, f-1(y) =
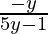
how to know if it is an inverse function
Source: https://www.geeksforgeeks.org/inverse-functions/
Posting Komentar untuk "how to know if it is an inverse function"